本当かな?シミュレーション Part2
さまざまな光学現象を理論で理解しようとすると、なかなか大変。
でもとりあえずシミュレーションで様子を見てみると、何だかちょっと分かったような気がするかも…。
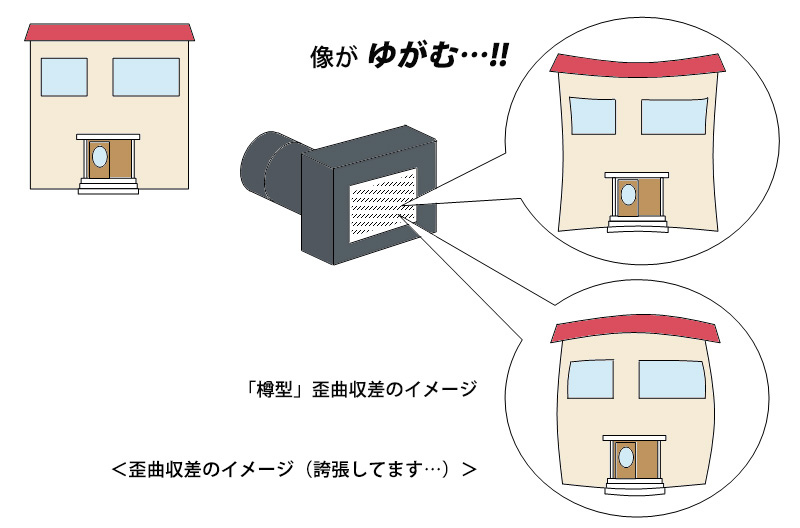
歪曲(わいきょく)収差は広義の球面収差の一つで、レンズ等によって作られる像が歪(ゆが)んでしまう現象です。建物の写真などで、写真の周辺部の柱や梁や壁などが少し曲がっているのを見かけることがありますが、それが歪曲収差です。一般的にカメラレンズは各種の収差がよく補正されていますし、レンズの「絞り」を絞る(開口を小さくする)と、僅かに残っている球面収差(狭義の)やコマ収差は更に小さくなります。また焦点深度も深くなるので、画質が向上するのですが、歪曲収差に関しては絞っても効果がなく、そういう意味で厄介な収差といえます。
この一見すると不思議な感じの歪曲収差は、カメラレンズのように光学系が複雑だから発生するというものでもなく、虫メガネのような身近にある単純な1枚のレンズでも、絞りの作用によって起きることが、文献に示されています。そこでこの1枚のレンズ(*)でも起きる歪曲収差を、シミュレーションソフトを使って見てみたいと思います。
(*注)正しくは“薄肉レンズ”です。
参考文献に記されている歪曲収差の基本的な原理です。
『 絞りのない(=絞りがレンズに一致している)薄肉レンズでは主光線はいつもその中心を通るから屈折をせず、屈折前後の光軸となす角度が変わらないので、歪曲収差がない。絞りが屈折面の前面にある薄肉レンズを考えると、球面収差の為に屈折光は収差のない場合より常にレンズより近い所で光軸と交わる。(略)そこで、この場合レンズの歪曲はいつでも負(樽型)で、絞りがレンズの後方にあれば、同様の考え方で正の歪曲(糸巻型)となる。
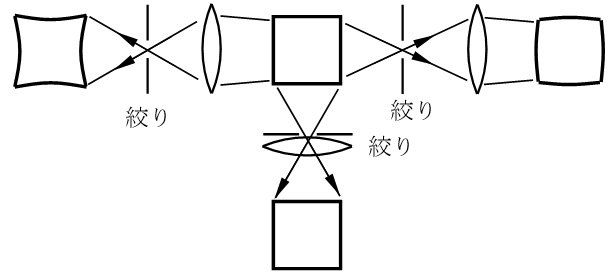
*以上、参考文献「光学」12-4レンズの歪曲収差 より抜粋(一部要約)。図は模写(一部簡略化)』
では、シミュレーションソフト「ZEMAX®」を使ってこの現象を起こしてみることにしましょう。
シミュレーションの条件は下記のようにしました。
○波長:550nm
○凸レンズ:焦点距離50mmのレンズ(石英製φ25.0、f50.0、fb48.02、Ct5.66、r1=r2=44.94)
○像倍率:等倍
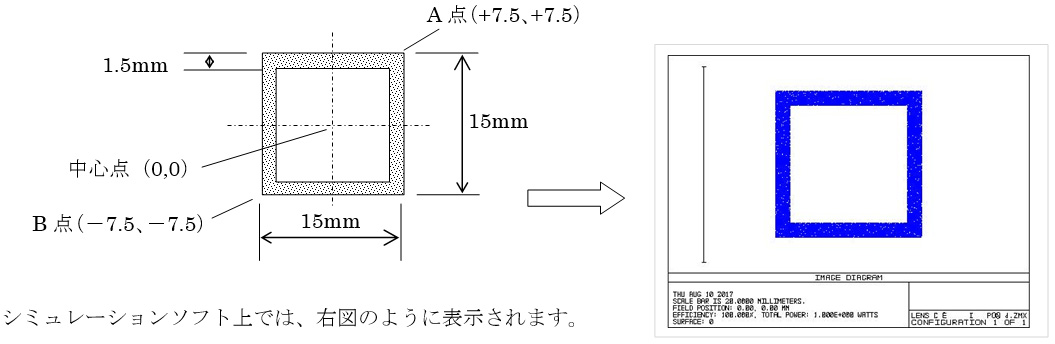
○被写体(物体):正方形の枠(1辺15mm、線の太さ1.5mm)(下図)
では、参考文献の図のように絞りをレンズの前方に置いた場合、後方に置いた場合に出来る像をシミュレーションし、歪曲収差が起きる様子を見てみましょう。
1.絞りの位置を変えると像はどうなる?
開口絞りを配置する位置を変え、そのとき出来る像を調べました。
尚、開口絞りの大きさは、それぞれの配置で、レンズ面上の有効径が同じになるようにφ5とφ2.5の2種類を選択して設定しました。
1.1絞りをレンズ前方に置いたときの像
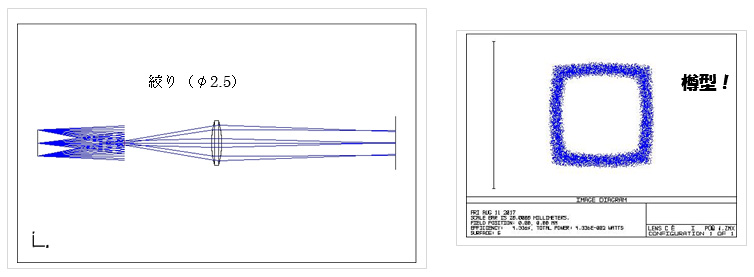
樽型歪曲収差が起きました。
1.2 絞りをレンズと同じ位置に置いたときの像
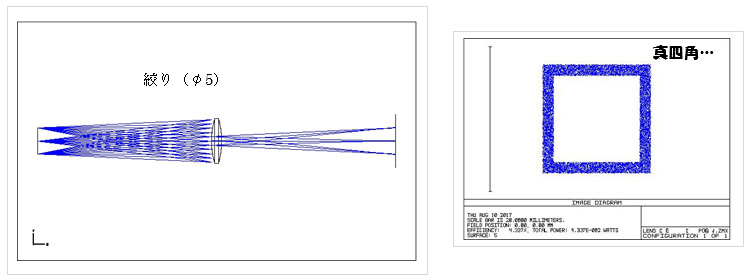
正確な形です。
1.3 絞りをレンズの後方に置いたときの像
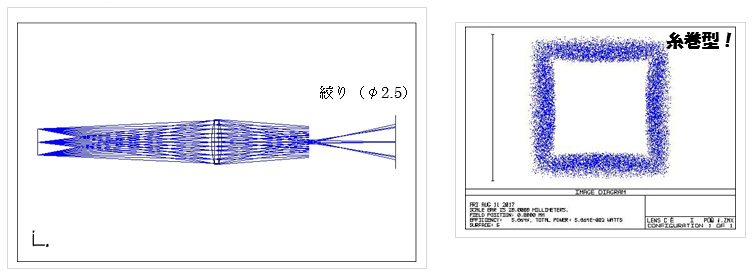
糸巻型歪曲収差が起きました。
本当に(実はシミュレーションですが…)歪曲収差が起きるんですね!!
それでは、絞りを絞っても効果がない(!?)ことを調べてみましょう。
1.4絞りを絞ったときの像の変化
配置例として、絞りをレンズ前方に置いた場合(前ページP3「1.1」)で調べます。
絞り開口:φ2.5(前ページ「1.1」の像と同じです。(分かりすくするために光線を多く飛ばしています。)
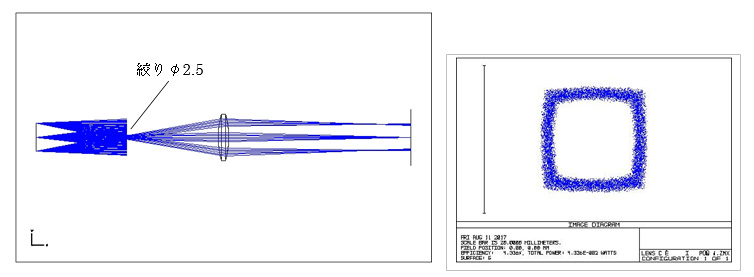
絞り開口 上図の1/2:φ1.25。像の枠の幅が少し狭くなりますが、歪曲収差が現れています。
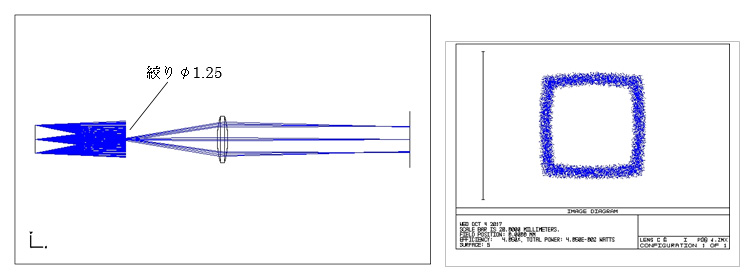
絞り開口 1/10:φ0.25。像の枠の輪郭がハッキリしますが、歪曲収差はやはり現れます。
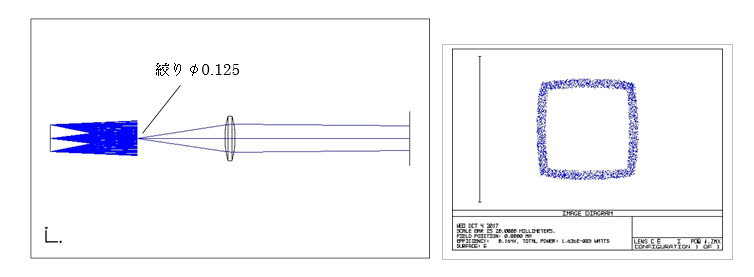
絞りを絞っても歪曲収差は消えないようですね。
それでは、この現象の主役ともいうべき“主光線”の様子を見てみましょう。
2.絞りの位置で主光線がどう変わるのか
下図は、被写体(物体)の上端から出る光の追跡図です。開口絞りを通過する光の中心が”主光線”です。
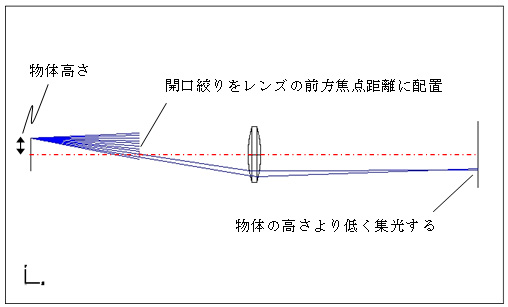
2.1開口絞りをレンズの前方焦点距離に配置
左図(2.1)で、開口絞りをレンズの前方焦点距離に配置した場合、開口絞りを通過する光線は、理想的レンズでは屈折して光軸に平行になりますが、実際のレンズでは球面収差(狭義)によって、図のように、より大きく屈折してしまいます。
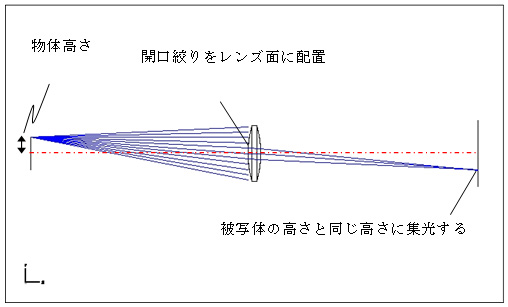
2.2開口絞りをレンズと同じ位置に配置
左図(2.2)で、開口絞りをレンズと同じ位置に配置した場合は、開口を通る光はレンズのほぼ中心を通ることになるので、実際のレンズでも入射角度と出射角度は、等しくなります。
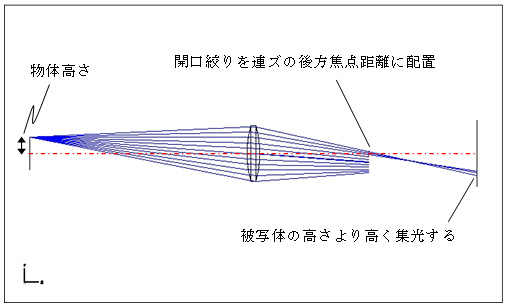
2.3開口絞りをレンズの後方焦点距離に配置
左図(2.3)で、開口絞りをレンズの後方焦点距離に配置した場合は、理想的レンズでは、光軸に平行にレンズに入射した光が開口絞りを通りますが、実際のレンズでは球面収差(狭義)により、少し拡がり気味に入射した光が通過します。
つまり、主光線が球面収差(狭義)によって、より深く屈折する現象が、歪曲収差を引き起こす、ということのようです。
なんだか少し分かったような気がしませんか?
最後に、球面収差(狭義)の例を、同じ球面レンズ、同じ波長(550nm)でシミュレーションしてみます。
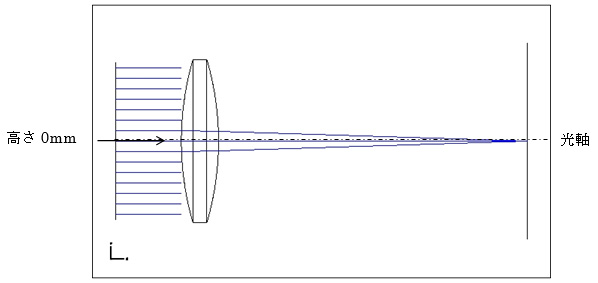
3.1光軸上の光
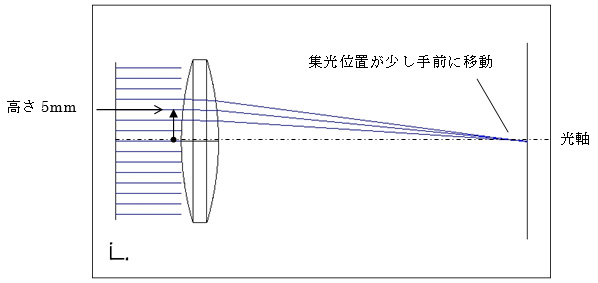
3.2光軸から5mmの高さの光
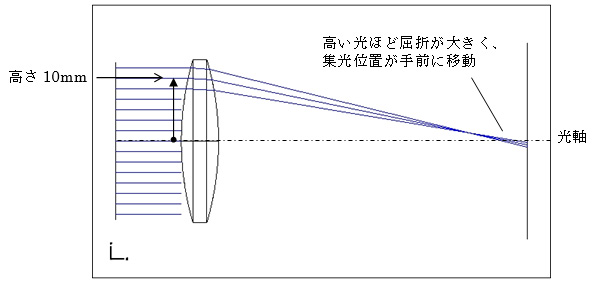
3.3光軸から10mmの高さの光
中心から離れた光ほど大きく屈折する・・・
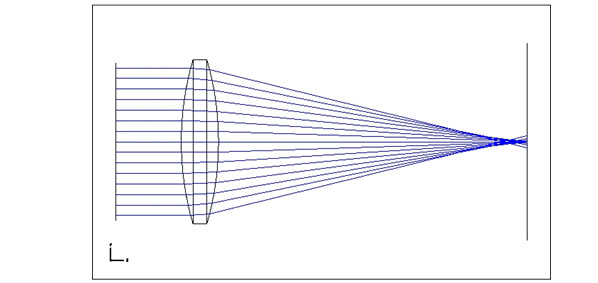
3.4全光束
最後の図は「狭義の球面収差」の説明でよく目にします。このよく知られた収差が、開口絞りと組み合わされると、歪曲収差という一見不思議な現象を引き起こす、というのも面白いですね。